Question

You have a bag of marbles with 10 green marbles and 12 black marbles. What is the probability that you pick a black marble on the first try. Do not replace that marble and pick a green marble on the second try?

Answer 1

20/77 or 0.26 or 26%

Explanation:

Extracting the key information from the question:-

*** There's a bag containing 10 green and 12 black marbles.

*** We are simply required to find the probability of picking a black marble first and then a green marble(NOT THE RESPECTIVE CHANCES).

The chance of picking a black marble is:

Number of black marbles/total number of marbles

=
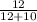`(12)/(12+10)`= 12/22

The chance of picking a green marble is:

Number of green marbles/total number of marbles

=
`(10)/(10+12)`

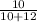
= 10/22

Note that when a marble is picked without replacing it, the total number of marbles available for further picking will reduce by one.

Now, without replacement, the probability of picking a black marble on the first attempt and a green marble on the second attempt is:

P(black, then green)[without replacement]

=
`(12)/(22) *(10)/(21)`

= 120/462

= 20/77 or 0.26 or 26%

Answer 2

Answer: 6/11 and 10/21

Explanation:

A bag of marbles has 10 green marbles and 12 black marbles. The probability of picking a black marble on the first try will be:

Green marbles= 10

Black marbles= 12

Total marbles= 12+10 = 22

Probability of picking a black marble = 12/22 = 6/11

If the marble is not replace, the probability of picking a green marble on the second try will be:

Green marbles= 10

Black marbles= 12-1= 11

Total marbles= 10+11= 21

Probability of picking a green marble= 10/21