Question

Solenoid A has total number of turns N length L and diameter D. Solenoid B has total number of turns 2N, length 2L and diameter 2D. Inductance of solenoid A is

8 times inductance of solenoid B
1/4 of inductance of solenoid B
same as inductance of solenoid B
1/8 of inductance of solenoid B
four times of inductance of solenoid B

Answer 1

Hi there!

We can begin by calculating the inductance of a solenoid.

Recall:

`L = (\Phi _B)/(i)`

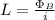
L = Inductance (H)
φ = Magnetic Flux (Wb)

i = Current (A)

We can solve for the inductance of a solenoid. We know that its magnetic field is equivalent to:

`B = \mu _0 (N)/(L)i`

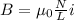
And that the magnetic flux is equivalent to:

`\Phi _B = \int B \cdot dA = B \cdot A`

Thus, the magnetic flux is equivalent to:

`\Phi _B = \mu _0 (N)/(L)iA`

The area for the solenoid is the # of loops multiplied by the cross-section area, so:

`A_(total)= N * A`

`\Phi _B = \mu _0 (N^2)/(L)iA`

Using this equation, we can find how it would change if the given parameters are altered:

`\Phi_B ' = \mu_0 ((2N)^2)/(2L) i * 4A`

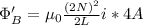
**The area will quadruple since a circle's area is 2-D, and you are doubling its diameter.

`\Phi'_B = (4)/(2) * 4(\mu_0 (N)/(L)iA) = 8\mu_0 (N)/(L)iA`

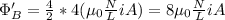
Thus, Solenoid B is 8 times as large as Solenoid A.

Solenoid A is 1/8 of the inductance of solenoid B.

Answer 2

∴Inductance of solenoid A is
`\frac18` of inductance of solenoid B.

Step-by-step explanation:

Inductance of a solenoid is

`L=N\frac\phi I`

`=N(B.A)/(I)`

`=N(\mu_0NI)/(l.I)A`

`=(\mu_0N^2A)/(l)`

`=(\mu_0N^2)/(l).\pi(\frac d2)^2`

`=\mu_0\pi(N^2d^2)/(4l)`

N= number of turns

`l` = length of the solenoid

d= diameter of the solenoid

A=cross section area

B=magnetic induction

`\phi` = magnetic flux

`I`= Current

Given that, Solenoid A has total number of turns N, length L and diameter D

The inductance of solenoid A is

`=\mu_0\pi(N^2D^2)/(4L)`

Solenoid B has total number of turns 2N, length 2L and diameter 2D

The inductance of solenoid B is

`=\mu_0\pi((2N)^2(2D)^2)/(4.2L)`

`=\mu_0\pi(16 N^2D^2)/(4.2L)`

Therefore,

`\frac {\textrm{Inductance of A}}{\textrm{Inductance of B}}=(\mu_0\pi(N^2D^2)/(4L))/(\mu_0\pi(16 N^2D^2)/(4.2L))`

`\Rightarrow \frac {\textrm{Inductance of A}}{\textrm{Inductance of B}}=\frac18`

`\Rightarrow {\textrm{Inductance of A}}=\frac18* {\textrm{Inductance of B}}`

∴Inductance of solenoid A is
`\frac18` of inductance of solenoid B.