Here is the correct question
A rotating wheel requires a time Δt = 4.28 seconds to rotate 37.0 revolutions. Its angular speed at the end of 4.28 seconds interval is ω = 75.9 rad/s. What is the constant angular acceleration (rad/s² ) of the wheel?
Answer:
10.09 rad/s²
Step-by-step explanation:
Given that :
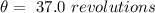
Then since 1 revolution =
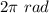
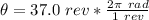
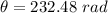
The first equation of motion for wheel can be expressed as :
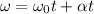
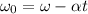
where
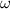 = 75.9 rad/s
= 75.9 rad/s
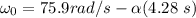
From the second equation of the motion
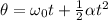
where ;
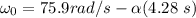
t = 4.28 s
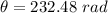
Then
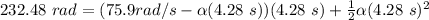
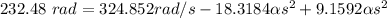
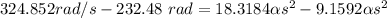
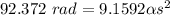
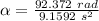
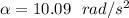
Thus, the angular acceleration of the wheel = 10.09 rad/s²