Answer:
3+7x
Explanation:
-We add the number of widgets produced in 3 days to the number originally owned:
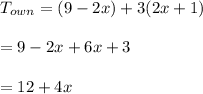
#We the determine the widgets destroyed in 3 days:
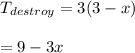
#Subtract the widgets destroyed from the total owned to get what is left after 3 days:
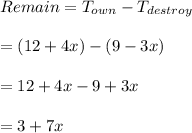
Hence, the number of widgets remaining after 3 days is 3+7x