Answer:
Yes, The events A and B are mutually exclusive event.
Explanation:
Two chips are drawn at random and without replacement from a bag containing two blue chips and two red chips.
Total chips (n ) = 4
Two chips are chooses from 4 chips then the total possibilities are =
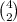
total outcomes =
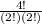 = 6
= 6
Let
 and
and
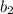 denote blue chips and
denote blue chips and
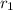 and
and
 denote red chips.
denote red chips.
A: {At least one of the chips is blue} = {

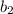 ,
,
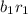 ,
,
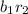 ,
,
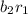 ,
,
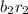 }
}
P( A) =

B: {Both chips are red} = {
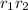 }
}
P( B) =

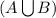 = {
= {
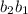 ,
,
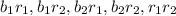 }
}
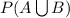 =
=
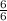
If A and B are mutuall exclusive
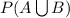 = P( A) + P( B)
= P( A) + P( B)
P( A) + P( B) =
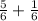 = 1
= 1
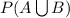 =
=
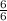 = 1
= 1
Hence
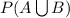 = P( A) + P( B)
= P( A) + P( B)
Then A and B are mutuall exclusive