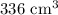Answer:
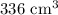
Explanation:
GIVEN: A wooden model of a square pyramid has a base edge of
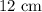 and an altitude of
and an altitude of
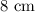 . A cut is made parallel to the base of the pyramid that separates it into two pieces: a smaller pyramid and a frustum. Each base edge of the smaller pyramid is
. A cut is made parallel to the base of the pyramid that separates it into two pieces: a smaller pyramid and a frustum. Each base edge of the smaller pyramid is
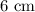 and its altitude is
and its altitude is
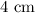 .
.
TO FIND: Volume of frustum.
SOLUTION:
Base edge of bigger square pyramid
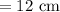
Altitude of bigger square pyramid
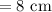
area of square base
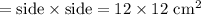
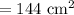
Volume of pyramid
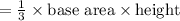
putting values

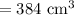
Base edge of smaller pyramid
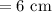
Altitude of smaller pyramid
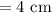
area of square base
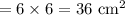
Volume of small pyramid
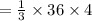
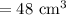
Volume of frustum
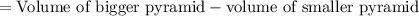
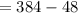
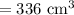
Hence the volume of frustum is