Question

A ball of mass 0.160 kg is dropped from a height of 2.25 m. When it hits the ground it compresses 0.087 m.

(A) What is its final velocity when it reaches the floor?
(B) What is the time of impact?
(C) What force does the floor exert on the ball?

Answer 1

A) 6.64 m/s downward

B) 0.026 s

C) -40.9 N

Step-by-step explanation:

A)

We can solve this problem by using the law of conservation of energy.

In fact, since the total mechanical energy of the ball must be conserved, this means that the initial gravitational potential energy of the ball before the fall is entirely converted into kinetic energy just before it reaches the floor.

So we can write:

`PE=KE\\mgh = (1)/(2)mv^2`

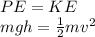
where

m = 0.160 kg is the mass of the ball

`g=9.8 m/s^2` is the acceleration due to gravity

h = 2.25 m is the initial height of the ball

v is the final velocity of the ball before hitting the ground

Solving for v, we find:

`v=√(2gh)=√(2(9.8)(2.25))=6.64 m/s`

And the direction of the velocity is downward.

B)

The motion of the ballduring the collision is a uniformly accelerated motion (= with constant acceleration), so the time of impact can be found by using a suvat equation:

`s=((u+v)/(2))t`

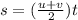
where:

v is the final velocity

u is the initial velocity

s is the displacement of the ball during the impact

t is the time

Here we have:

u = 6.64 m/s is the velocity of the ball before the impact

v = 0 m/s is the final velocity after the impact (assuming it comes to a stop)

s = 0.087 m is the displacement, as the ball compresses by 0.087 m

Therefore, the time of the impact is:

`t=(2s)/(u+v)=(2(0.087))/(0+6.64)=0.026 s`

C)

The force exerted by the floor on the ball can be found using the equation:

`F=(\Delta p)/(t)`

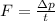
where

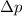`\Delta p` is the change in momentum of the ball

t is the time of the impact

The change in momentum can be written as

`\Delta p = m(v-u)`

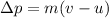
So the equation can be rewritten as

`F=(m(v-u))/(t)`

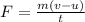
Here we have:

m = 0.160 kg is the mass of the ball

v = 0 is the final velocity

u = 6.64 m/s is the initial velocity

t = 0.026 s is the time of impact

Substituting, we find the force:

`F=((0.160)(0-6.64))/(0.026)=-40.9 N`

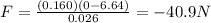
And the sign indicates that the direction of the force is opposite to the direction of motion of the ball.