Question

4. The distribution of blood cholesterol level in the population of young men aged 20 to 34 years is close to Normal, with mean 188 milligrams per deciliter and standard deviation 41 mg/dl. a. Find the probability that a young man (aged 20 to 34) has a cholesterol level greater than 200 milligrams per deciliter. b. Suppose you measure the cholesterol level of 100 young men chosen at random and calculate the sample mean. If you did this many times, i. what would be the mean of the distribution of the sample mean

Answer 1

a) 38.59% probability that a young man (aged 20 to 34) has a cholesterol level greater than 200 milligrams per deciliter.

b) By the Central Limit Theorem, the mean of the distribution of the sample mean would be 188 milligrams per deciliter

Explanation:

Problems of normally distributed samples are solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

In this problem, we have that:

`\mu = 188, \sigma = 41`

a. Find the probability that a young man (aged 20 to 34) has a cholesterol level greater than 200 milligrams per deciliter.

This is 1 subtracted by the pvalue of Z when X = 200. So

`Z = (X - \mu)/(\sigma)`

`Z = (200 - 188)/(41)`

`Z = 0.29`

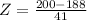
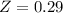
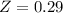`Z = 0.29` has a pvalue of 0.6141

1 - 0.6141 = 0.3859

38.59% probability that a young man (aged 20 to 34) has a cholesterol level greater than 200 milligrams per deciliter.

b. Suppose you measure the cholesterol level of 100 young men chosen at random and calculate the sample mean. If you did this many times, i. what would be the mean of the distribution of the sample mean

By the Central Limit Theorem, the mean of the distribution of the sample mean would be 188 milligrams per deciliter