Question

HELPP GUYSSS ::: Consider the functions:

ƒ(x) = 0.25x + 25 and g(x) = 15(1.25)x

As x approaches ∞, which statement is correct?
A) The linear function will always exceed the exponential function.
B) The exponential function will always exceed the linear function.
C) The linear function will exceed the exponential function since its initial value is greater.
D) The exponential function will exceed the linear function since its base is greater than one.

Answer 1

B) The exponential function will always exceed the linear function.

(On USATP)

Explanation:

Exponential functions would eventually exceed the any other function. They grow at a more faster rate than linear or quadradic functions. Exponential functions are the fastest growing functions.

If the base was less than one then the x-values would approach zero, but in general terms exponential functions will eventually exceed the linear function.

Hope this helps.

PS: [see picture attached]

Answer 2

Correct option D) Base of exponential function
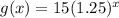`g(x) = 15(1.25)^x` is greater than 1 , this function will exceed linear function
`f(x) = 0.25x + 25` .

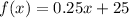Explanation:

Here we have , f(x) = 0.25x + 25 and g(x) = 15(1.25)x . We need to tell As x approaches ∞, which function exceeds whom! Let's find out:

• f(x) = 0.25x + 25

This function is a linear function with an equation of straight line , having slope and y-intercept as :

`m=0.25\\c=25`

Graph for this function is attached below .

• g(x) = 15(1.25)^x

This function is an exponential function in the form of
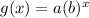`g(x) = a(b)^x` , where b>1 i.e. for rise in value of x there is exponential increase in value of y or , function .Basically Base of this exponential is greater than 1 , which makes it an increasing function ! Graph for this function is attached below .

Now , Comparing both graphs we see that as x approaches ∞ graph of exponential function
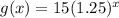`g(x) = 15(1.25)^x` is much more vertical than linear function
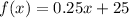`f(x) = 0.25x + 25` . Since , base of exponential function
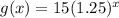`g(x) = 15(1.25)^x` is greater than 1 , this function will exceed linear function
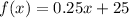`f(x) = 0.25x + 25` .Correct option D)