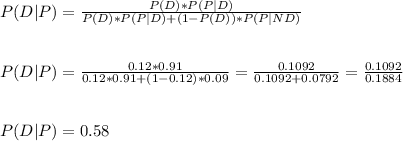Question

(10 points) A test for a certain drug produces a false negative 3% of the time and a false positive 9% of the time. Suppose 12% of the employees at a certain company use the drug. If an employee at the company tests negative, what is the probability that he or she does use the drug

Answer 1

If an employee at the company tests negative, the probability that he or she does use the drug is P=0.58.

Explanation:

We have this information:

proportion of drug users P(D)=0.12

false negatives FN=P(N|D)=0.03 --> True negatives P(N|ND)=0.97

false positives FP=P(P|ND)=0.09 --> True positives P(P|D)=0.91

where:

D: drug user

ND: no drug user

N: negative result

P: positive result

We have to calculate the probability that, given a positive teste, the person is a drug user.

Applying the Bayes theorem, we have:

`P(D|P)=(P(D)*P(P|D))/(P(D)*P(P|D)+(1-P(D))*P(P|ND))\\\\\\P(D|P)=(0.12*0.91)/(0.12*0.91+(1-0.12)*0.09)=(0.1092)/(0.1092+0.0792)=(0.1092)/(0.1884)\\\\\\P(D|P)= 0.58`