Question

6. Bons grocer wishes to mix some nuts worth 90 cents per pound with some nuts worth $1.60 per pound to make 175 pounds of a mixture that is worth $1.30 per pound. How much of each should she use? Include your equation. *

Answer 1

75 pounds and 100 pounds.

Explanation:

Given:

Bons grocer wishes to mix some nuts worth 90 cents( $0.9) per pound with some nuts worth $1.60 per pound to make 175 pounds of a mixture that is worth $1.30 per pound.

Question asked:

How much of each should she use?

Solution:

Let there are two types of nuts mixed in the mixture, one is nut A and another is nut B.

As we know:

1 cent = $0.01

90 cents = $0.01
`*` 90 = $0.9

Let quantity of nut A mixed =
`x\ pound`

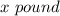
Quantity of nut B mixed =
`175-x\ pound`

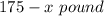
Total quantity of mixture = 175 pounds

Total cost of mixture = Cost per pound
`*` Total quantity of mixture in pound

= $1.30
`*` 175 = $227.5

As mixture is prepared by mixing two types of nuts:-

Cost per pound of nut A
`*` Quantity mixed + Cost per pound of nut B

`0.9x+1.60(175-x)=227.5\\0.9x+280-1.60x=227.5\\-0.7x+280=227.5\\`

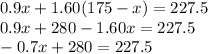
By subtracting both sides by 280

`-0.7x=-52.5`

Minus canceled by minus

`0.7x=52.5\\Dividing\ both\ sides\ by\ 0.7\\x=75\ pound`

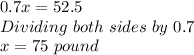
Substituting the value:-

Quantity of nut A mixed =
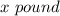`x\ pound` = 75 pounds

Quantity of nut B mixed =
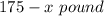`175-x\ pound`= 175 - 75 = 100 pounds

Therefore, Bons grocer wishes to mix 75 pounds of nuts worth 90 cents ($0.9) with 100 pounds of some nuts worth $1.60 per pound to make 175 pounds of a mixture that is worth $1.30 per pound.

Answer 2

The quantity of first mixture = x = 75 pounds

The quantity of second mixture = 175 - x = 175 - 75 = 100 pounds

Explanation:

Total quantity of mixture = 175 pounds

Let quantity of first mixture = x

Quantity of second mixture = 175 - x

From the given information

x (0.9) + (175 - x) × 1.6 = 175 × 1.3

By solving above equation we get

0.9 x + 280 - 1.6 x = 227.5

0.7 x = 52.5

x = 75 pounds

Thus the quantity of first mixture = x = 75 pounds

The quantity of second mixture = 175 - x = 175 - 75 = 100 pounds