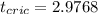Answer:
a)
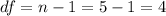
For this case the significance level is given by
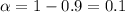 and the
and the
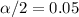 and for this case we can ue the following code:
and for this case we can ue the following code:
"=-T.INV(0.05,4)"
And for this case the critical value would be
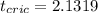
b)

For this case the significance level is given by
 and the
and the
 and for this case we can ue the following code:
and for this case we can ue the following code:
"=-T.INV(0.025,12)"
And for this case the critical value would be
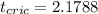
c)

For this case the significance level is given by
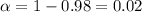 and the
and the
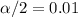 and for this case we can ue the following code:
and for this case we can ue the following code:
"=-T.INV(0.01,21)"
And for this case the critical value would be
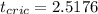
d)
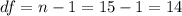
For this case the significance level is given by
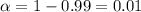 and the
and the
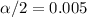 and for this case we can ue the following code:
and for this case we can ue the following code:
"=-T.INV(0.005,14)"
And for this case the critical value would be
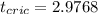
Explanation:
Part a
n = 5 , Conf. =0.90
For this case the degrees of freedom are given by:
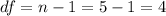
For this case the significance level is given by
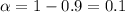 and the
and the
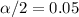 and for this case we can ue the following code:
and for this case we can ue the following code:
"=-T.INV(0.05,4)"
And for this case the critical value would be
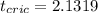
Part b
n = 13 , Conf. =0.95
For this case the degrees of freedom are given by:

For this case the significance level is given by
 and the
and the
 and for this case we can ue the following code:
and for this case we can ue the following code:
"=-T.INV(0.025,12)"
And for this case the critical value would be
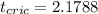
Part c
n = 22 , Conf. =0.98
For this case the degrees of freedom are given by:

For this case the significance level is given by
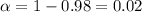 and the
and the
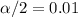 and for this case we can ue the following code:
and for this case we can ue the following code:
"=-T.INV(0.01,21)"
And for this case the critical value would be
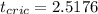
Part d
n = 15 , Conf. =0.99
For this case the degrees of freedom are given by:
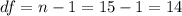
For this case the significance level is given by
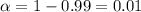 and the
and the
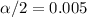 and for this case we can ue the following code:
and for this case we can ue the following code:
"=-T.INV(0.005,14)"
And for this case the critical value would be