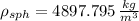Answer:
a)
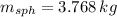 , b)
, b)
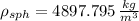
Step-by-step explanation:
According to the Archimedes' Principle, the buoyancy force is equal the weight of the displaced fluid. Then, this equation of equilibrium is constructed by the Newton's Laws:
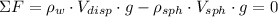
After some algebraic handling:
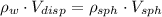
a) The mass of the sphere is:
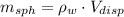
![m_(sph) = (927\,(kg)/(m^(3)) )\cdot \left[(4)/(3)\pi\cdot (0.099\,m)^(3) \right]](https://img.qammunity.org/2021/formulas/physics/college/3nyo1vfrs02ngpo4je4swhbge3lr6u6z2b.png)
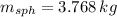
b) The density of the sphere is:
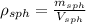
![\rho_(sph) = (3.768\,kg)/((4)/(3)\pi\cdot [(0.099\,m)^(3)-(0.087\,m)^(3)])](https://img.qammunity.org/2021/formulas/physics/college/ye7bq0a7akncpl25yln97nuvjv75dosiuo.png)