Question

Marisol is designing a system to detect when the door to her room is opened. She has observed that the magnetic field in the vicinity of the door is perpendicular to the door when it is closed and has a magnitude of about B = 5.50 × 10 − 5 T. B=5.50×10−5 T. Knowing Faraday's law, Marisol uses electromagnetic induction as the basis of her alarm. She wraps a single loop of wire around the perimeter of her door and connects it to a voltmeter that can detect an emf as small as V min = 1.00 × 10 − 6 V. Vmin=1.00×10−6 V. The voltmeter is configured to take a time‑averaged reading and will trigger the alarm if the average emf over a certain period of time exceeds the threshold voltage V min . Vmin. What is the minimum time interval t min tmin required for someone to open Marisol’s door θ = 34.0 ∘ , θ=34.0∘, starting from the closed position, without the average induced emf over that time interval exceeding the threshold? The dimensions of the door are W = 0.895 m W=0.895 m by H = 2.15 m.

Answer 1

The minimum time interval required is 18.1 sec

Step-by-step explanation:

Given:

Magnetic field
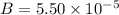`B = 5.50 * 10^(-5)` T

Minimum induced emf
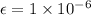`\epsilon = 1 * 10^(-6)` V

Angle between magnetic field and area vector
`\theta =` 34°

Area of door
`A = 0.895 * 2.15 = 1.924`
`m^(2)`

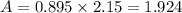
According to the faraday's law,

`\epsilon = -(d\phi)/(dt)`

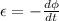
Where
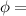`\phi =` magnetic flux

From the formula of magnetic flux,

`\phi = BA\cos \theta`

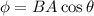
Initially,

`\phi _(i) = BA\cos 34`

`= 5.50 * 10^(-5) * 1.924 * 0.8290`

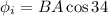
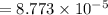`= 8.773 * 10^(-5)` Wb

When door is closed,

`\phi _(f) = BA\cos 0`

`= 5.50 * 10^(-5) * 1.924`

`\phi _(f) = 10.58 * 10^(-5)` Wb

Hence
`d\phi = \phi _(f) - \phi _(i)`

`d\phi = (10.58 - 8.773 ) * 10^(-5)`

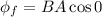
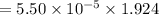
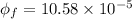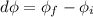
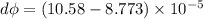
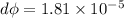`d \phi = 1.81 * 10^(-5)` Wb

Put the values in above equation,

`dt = (d \phi)/(\epsilon)`

`dt = (1.81 * 10^(-5) )/(1 * 10^(-6) )`

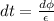
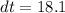`dt = 18.1` sec

Therefore, the minimum time interval required is 18.1 sec