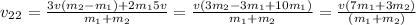Answer:
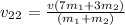
Step-by-step explanation:
The collision between two or more bodies is said to be elastic when the total kinetic energy of the body system is conserved during the interaction. During it, the amount of movement, momentum or linear momentum of the system, is also conserved. Therefore we can assume the following:
Conservation of linear momentum:
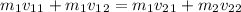 (1)
(1)
Kinetic energy conservation:
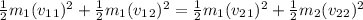 (2)
(2)
Where:

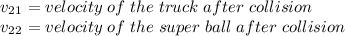
Solving the 2x2 system of equations:
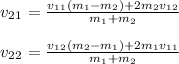
Therefore, the approximate speed of the super ball after the collision is: