Question

A tank contains 8000 L of pure water. Brine that contains 35 g of salt per liter of water is pumped into the tank at a rate of 25 L/min. The concentration of salt after t minutes (in grams per liter) is C(t) = 35t 320 + t . As t → [infinity], what does the concentration approach?

Answer 1

The concentration of salt in the tank approaches
`35 \mathrm{g} / \mathrm{L},`

Explanation:

Data provide in the question:

Water contained in the tank = 8000 L

Salt per litre contained in Brine = 35 g/L

Rate of pumping water into the tank = 25 L/min

Concentration of salt
`\lim _(t \rightarrow \infty) C(t)=\lim _(t \rightarrow \infty) (35 t)/(320+t)`

Now,

Dividing both numerator and denominator by
`t`, we have

`\lim _(t \rightarrow \infty) ((1)/(t) 35 t)/((1)/(t)(320+t))=\lim _(t \rightarrow \infty) (35)/((320)/(t)+1)=35`

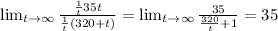
Here,

The concentration of salt in the tank approaches
`35 \mathrm{g} / \mathrm{L},`