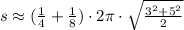Answer:
a) See the file below, b)
![s = \int\limits^(0.5\pi)_(-0.25\pi) {[\left( 3\cdot \cos t\right)^(2)+\left(-5\cdot \sin t \right)^(2)]} \, dx](https://img.qammunity.org/2021/formulas/mathematics/college/e9dnbu73c200491ti7sf3ukpa5shar3c8x.png) , c)
, c)

Explanation:
a) Points moves clockwise as t increases. See the curve in the file attached below. The parametric equations describe an ellipse.
b) The arc length formula is:
![s = \int\limits^(0.5\pi)_(-0.25\pi) {[\left( 3\cdot \cos t\right)^(2)+\left(-5\cdot \sin t \right)^(2)]} \, dx](https://img.qammunity.org/2021/formulas/mathematics/college/e9dnbu73c200491ti7sf3ukpa5shar3c8x.png)
c) The perimeter of that arc is approximately: