Question

If the slope of a line is 4/5, does the line rise (from left to right), fall (from left to right), horizontal or vertical?

Answer 1

rise from left to right

Explanation:

Linear equation:
`y=mx+b`

(where
`m` is the slope and
`b` is the y-intercept)

Positive slope: rise from left to right

`m` is a positive number

`\textsf{e.g.}\:y=\frac45x+4`

Negative slope: fall from left to right

`m` is a negative number

`\textsf{e.g.}\:y=-\frac45x+4`

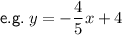
Zero slope: horizontal line

`m=0`

`\textsf{e.g.}\:y=0x+\frac45\implies y=\frac45`

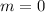
Therefore, a horizontal line is
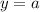`y = a` (where
`a` is some constant)

Infinite slope: vertical line

`m= \infty`

`\sf slope\: (m)=(change\:in\:y)/(change\:in\:x)`

There is no change in x-values for a vertical line, so:

`\sf \implies slope=(change\:in\:y)/(0)=\infty`

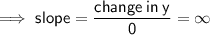
We also usually call the slope of this line undefined.

Therefore, a vertical line is
`x = a` (where
`a` is some constant)

---------------------------------------------------------------------------------

Attached graph:

Positive slope: black line

Negative slope: blue line

Zero slope: green line

Infinite slope: red line

Answer 2

slope: 4/5 is a positive slope

• positive slopes rises from left to right

• positive slopes falls from right to left

• neither horizontal or vertical.

The picture below shows some examples of equation with positive slope.