Answer:
The probability that the arrival time between customers will be 12 or less is 0.6027.
Explanation:
We are given that the time between arrivals of customers at the drive-up window of a bank follows an exponential probability distribution with a Mean of 13.
Let X = time between arrivals of customers
The probability distribution for exponential distribution is given by;
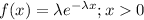
where,
 = parameter of this distribution or the arrival rate
= parameter of this distribution or the arrival rate
Since, the mean of exponential distribution = E(X) =
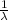
So, 13 =
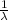 ,
,
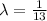
So, X ~ Exp(
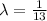 )
)
Now, to find the less than or greater than probabilities in exponential distribution we use the Cumulative distribution function of exponential function, i.e.;
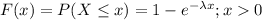
So, probability that the arrival time between customers will be 12 or less is given by = P(X
 12)
12)
P(X
 12) =
12) =

=
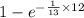
=
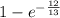 = 0.6027
= 0.6027
Therefore, probability that the arrival time between customers will be 12 or less is 0.6027.