Question

According to a​ report, 61.8​% of murders are committed with a firearm. ​(a) If 100 murders are randomly​ selected, how many would we expect to be committed with a​ firearm? ​(b) Would it be unusual to observe 69 murders by firearm in a random sample of 100 ​murders? Why?

Answer 1

a)
`E(X) = np = 100*0.618 = 61.8`

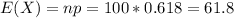
b) For this case the standard deviation would be:

`Sd(X) = √(np(1-p))= √(100*0.618*(1-0.618))= 4.859`

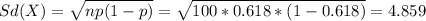
For this case if we use the rule of thumb we can expect that the uual values would be within two deviation from the mean so then the limits for the usual values are:

`Lower = 61.8- 2*4.859= 56.94`

`Upper = 61.8+ 2*4.859= 71.52`

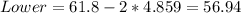
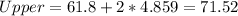
And since the value of 69 is contained on the interval we can't consider 69 as an unusual value for this case.

Explanation:

Previous concepts

The binomial distribution is a "DISCRETE probability distribution that summarizes the probability that a value will take one of two independent values under a given set of parameters. The assumptions for the binomial distribution are that there is only one outcome for each trial, each trial has the same probability of success, and each trial is mutually exclusive, or independent of each other".

Solution to the problem

Let X the random variable of interest, on this case we now that:

`X \sim Binom(n=100, p=0.618)`

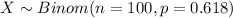
The probability mass function for the Binomial distribution is given as:

`P(X)=(nCx)(p)^x (1-p)^(n-x)`

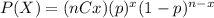
Where (nCx) means combinatory and it's given by this formula:

`nCx=(n!)/((n-x)! x!)`

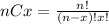
Part a

For this case the expected value would be given by:

`E(X) = np = 100*0.618 = 61.8`

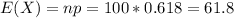
So we would expecte about 62 murders with a firearm

Part b

For this case the standard deviation would be:

`Sd(X) = √(np(1-p))= √(100*0.618*(1-0.618))= 4.859`

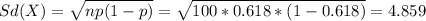
For this case if we use the rule of thumb we can expect that the uual values would be within two deviation from the mean so then the limits for the usual values are:

`Lower = 61.8- 2*4.859= 56.94`

`Upper = 61.8+ 2*4.859= 71.52`

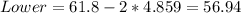
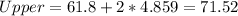
And since the value of 69 is contained on the interval we can't consider 69 as an unusual value for this case.