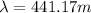Question

(a) the gamma rays produced by a radioactive nuclide used in medical imaging (b) radiation from an FM radio station at 93.1 MHz on the dial (c) a radio signal from an AM radio station at 680 kHz on the dial (d) the yellow light from sodium vapor streetlights (e) the red light of a light-emitting diode, such as in a calculator display Rank labels from high wavelength to low.

Answer 1

They can be rank in the following way:

• A radio signal from an AM radio station at 680 kHz on the dial

• Radiation from an FM radio station at 93.1 MHz on the dial

• The red light of a light-emitting diode, such as in a calculator

• The yellow light from sodium vapor streetlights

• The gamma rays produced by a radioactive nuclide used in medical

Step-by-step explanation:

The electromagnetic spectrum is the distribution of radiation due to the different frequencies at which it radiates and its different intensities, that radiation is formed by electromagnetic waves, which are transverse waves formed by an electric field and a magnetic field perpendicular to it.

Radiation is distributed along that electromagnetic spectrum according to the wavelength or frequency.

Highest frequencies

X-rays

Ultraviolet rays

Visible region

Lower frequencies

Infrared

Microwave

Radio waves

Radio waves and the visible region (yellow light, red light) are part of the electromagnetic spectrum, any radiation of that electromagnetic spectrum has a speed of 3.00x10^{8}m/s in vacuum.

However, the following equation relates the velocity, the frequency, and the wavelength:

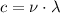`c = \\u \cdot \lambda` (1)

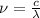`\\u = (c)/(\lambda)` (2)

It can be see in equation 2 that the frequency and the wavelength are inversely proportional (when the frequency increases the wavelength decreases).

Therefore, for what was already discussed, they can be rank in the next way:

• A radio signal from an AM radio station at 680 kHz on the dial

• Radiation from an FM radio station at 93.1 MHz on the dial

• The red light of a light-emitting diode, such as in a calculator

• The yellow light from sodium vapor streetlights

• The gamma rays produced by a radioactive nuclide used in medical

Summary:

In the case of the radio waves can be used:

Case for
`\\u = 93.1 MHz`:

`\lambda = (c)/(\\u)`

`\lambda = (3x10^(8)m/s)/(93100000s^(-1))`

`\lambda = 3.22m`

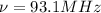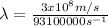
Case for
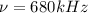`\\u = 680 kHz`:

`\lambda = (c)/(\\u)`

`\lambda = (3x10^(8)m/s)/(680000s^(-1))`

`\lambda = 441.17m`