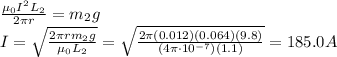Question

Two rigid rods are oriented parallel to each other and to the ground. The rods carry the same current in the same direction. The length of each rod is 1.1 m, while the mass of each is 0.064 kg. One rod is held in place above the ground, and the other floats beneath it at a distance of 12 mm. Determine the current in the rods.

Answer 1

185 A

Step-by-step explanation:

In order for the rod to float above the ground, the magnetic force between the two rods must be equal to the weight of the floating rod.

So we can write:

`(\mu_0 I_1 I_2 L_2)/(2\pi r)=m_2 g`

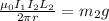
where the term on the left is the magnetic force and the term on the right is the weight, and where:

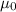`\mu_0` is the vacuum permeability

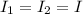`I_1 = I_2 = I` is the current in the two rods (they carry the same current)

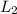`L_2` is the length of the floating rod

r is the distance between the rods

`m_2` is the mass of the floating rod

g is the acceleration due to gravity

Here we have:

`L_2 = 1.1 m`

`m_2=0.064 kg`

`r=12 mm = 0.012 m`

`g=9.8 m/s^2`

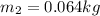
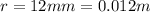
Therefore, solving for I, we find:

`(\mu_0 I^2 L_2)/(2\pi r)=m_2 g\\I=\sqrt{(2\pi r m_2 g)/(\mu_0 L_2)}=\sqrt{(2\pi(0.012)(0.064)(9.8))/((4\pi \cdot 10^(-7))(1.1))}=185.0 A`