Question

A 0.03-kg bullet is fired with a horizontal velocity of 470 m/s and becomes embedded in block B which has a mass of 3 kg. After the impact, block B slides on a 30-kg carrier C until it impacts the end of the carrier. Knowing the impact between B and C is perfectly plastic and the coefficient of kinetic friction between B and C is 0.2, determine the velocity of the bullet and block B after the first impact and the final velocity of the carrier. (Round the final answer answers to two decimal places.)

Answer 1

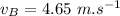`v_B=4.65\ m.s^(-1)` is the velocity of the block and the bullet system after the first impact.

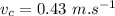`v_c=0.43\ m.s^(-1)` is the velocity of the carrier.

Step-by-step explanation:

Given

mass of bullet,
`m=0.03\ kg`

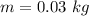
horizontal velocity of bullet,
`v=470\ m.s^(-1)`

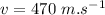
mass of block,
`m_B=3\ kg`

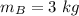
mass of carrier,
`m_c=30\ kg`

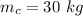
coefficient of kinetic friction between block and carrier,
`\mu_k=0.2`

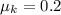
Since the collision between the bullet and the block is perfectly plastic:

We have the conservation of linear momentum as:

`m.v=(m+m_B).v_B=(m+m_B+m_c).v_c`

`0.03* 470=(0.03+3)* v_B=(0.03+3+30)* v_c`

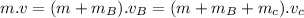
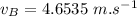`v_B=4.6535\ m.s^(-1)` is the velocity of the block and the bullet system after collision.

After the collision of block & carrier:

`v_c=0.4268\ m.s^(-1)` is the velocity of the carrier.

Answer 2

Answer with Explanation:

We are given that

Mass of bullet,
`m_1=0.03 kg`

`u_1=470 m/s`

`m_2=3 kg`

`\mu_k=0.2`

`m_3=30 kg`

We have to find the velocity of the bullet and block B after the first impact and final velocity of the carrier.

According to law of conservation of momentum

`m_1u_1=(m_1+m_2)v`

`0.03(470)=(0.03+3)v`

`v=(0.03(470))/((0.03+3))=4.65 m/s`

Hence, the velocity of the bullet and block B after the first impact=4.65 m/s

According to law of conservation of momentum

`(m_1+m_2)v=(m_1+m_2+m_3)V`

`(0.03+3)* 4.65=(0.03+3+30)V`

`V=((0.03+3)* 4.65)/((0.03+3+30))`

`V=0.43 m/s`