Answer:
Ethan's tangential speed is twice as Rebecca's.
Step-by-step explanation:
Let
 be the distance from the center of the platform to Rebecca's horse,
be the distance from the center of the platform to Rebecca's horse,
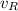 Rebecca's tangential speed,
Rebecca's tangential speed,
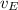 the Ethan's tangential speed and
the Ethan's tangential speed and
 the merry-go-round angular speed. The distance from the center of the platform to Ethan's horse is
the merry-go-round angular speed. The distance from the center of the platform to Ethan's horse is
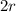 . The angular speed is related to the tangential speed by the equation:
. The angular speed is related to the tangential speed by the equation:
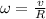
Since the angular speed is the same for Ethan and Rebecca, we have that:
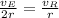
Now, solving for
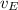 we get:
we get:

It means that Ethan's tangential speed is twice as Rebecca's.