Answer:
(1) The probability that the sample mean is Greater than 59 = 0.778
(2) The probability that the sample mean is less than 59 = .3632
(3) The probability that the sample mean is is Between 54 and 59 = 0.559
Explanation:
Given -
Mean
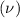 = 55
= 55
Standard deviation
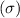 = 14
= 14
Sample size ( n ) = 25
the probability that the sample mean
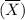 is Greater than 59 =
is Greater than 59 =
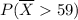 =
=
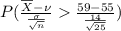
=
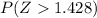
= 1 -
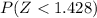
= 1 - 0.9222 = .0778
the probability that the sample mean
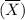 is Less than 54 =
is Less than 54 =
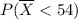 =
=
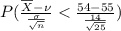
=
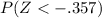
= .3632
the probability that the sample mean is Between 54 and 59 =
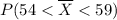 =
=
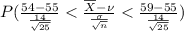
=
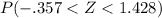
=
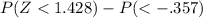
= .9222 - .3632
= 0.559