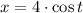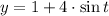Question

Find parametric equations for the path of a particle that moves along the circle x2 + (y − 1)2 = 16 in the manner described. (Enter your answer as a comma-separated list of equations. Let x and y be in terms of t.)

Answer 1

`x = 4\cdot \cos t`

`y = 1 + 4\cdot \sin t`

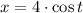
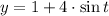
Explanation:

The parametric equations are determined by determining the trigonometric expressions associated to each component. Let 16 the square of the hypotenuse of a right-angled triangle, of which one of its extremes is set on the center of the circle C(0, 1). Then:

`(x^(2))/(16) + ((y-1)^(2))/(16) = 1`

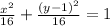
By remembering the fundamental trigonometric identity (
`\cos^(2) t + \sin^(2)t = 1`) and comparing it with each term, the parametric equations are finally found:

`x = 4\cdot \cos t`

`y = 1 + 4\cdot \sin t`