Question

Under many conditions, the center of mass of a system of particles can represent the system as a whole. But how far does this rule extend?

Consider two identical particles traveling toward each other at the same speed. By examining this system, choose the correct response.

a. The momentum and kinetic energy of the center of mass is equivalent to that of the system of particles.
b. The kinetic energy, but not the momentum, of the center of mass is equivalent to that of the system of particles.
c. Neither the momentum nor the kinetic energy of the center of mass is equivalent to that of the system of particles.
d. The momentum, but not the kinetic energy, of the center of mass is equivalent to that of the system of particles.

Answer 1

The correct answer is a

Step-by-step explanation:

The concept of center of mass strongly simplifies the analysis of problems, since all the external bridging forces = denote the point of the center ce plus.

xcm = 1 / M ∑xi mi

v cm = 1 / M ∑ xi vi

When we do this, the momentum and the kinetic energy are conserved, that is, it is equivalent to the movement of the particle system

The correct answer is a

Answer 2

d. The momentum, but not the kinetic energy, of the center of mass is equivalent to that of the system of particles.

Step-by-step explanation:

The center of mass is equal to:

`x_(cm) =(m_(1)x_(1)+m_(2)x_(2))/(m_(1)+m_(2) )` (eq. 1)

The total mass is:

mtotal = m₁ + m₂

Replacing:

`x_(cm) =(m_(1)x_(1)+m_(2)x_(2))/(m_(total) )\\x_(cm)*{m_(total) ={m_(1)x_(1)+m_(2)x_(2)} }` (eq. 2)

Differentiate respect to time is:

`(d)/(dt) x_(cm) m_(total) =(d)/(dt) m_(1) x_(1) +m_(2) x_(2)\\m_(total)v_(cm) =m_(1) v_(1)+m_(2) v_(2)`

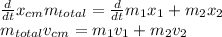
The momentum is:

`P_(cm) =m_(total) v_(cm) =m_(1) v_(1)+m_(2) v_(2)`

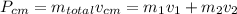
Differentiate the equation 1 respect to time is:

`(d)/(dt) x_(cm) =(d)/(dt) (m_(1)x_(1)+m_(2)x_(2))/(m_(total) )\\v_(cm) =(1)/(m_(total) ) {m_(1)v_(1)+m_(2)v_(2)} }`

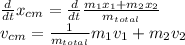
The kinetic energy is:

`E_(k) =(1)/(2) m_(total) v_(cm) ^(2) =(1)/(2m_(total) ) (m_(1)v_(1) -m_(2)v_(2))^(2)`

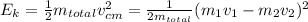
Observing equations 1 and 2, it can be seen that the kinetic energy of the center of mass is not equal to that of the particle system.