Question

Current research indicates that the distribution of the life expectancies of a certain protozoan is normal with a mean of 46 days and a standard deviation of 10.5 days. Find the probability that a simple random sample of 49 protozoa will have a mean life expectancy of 47 or more days.

Answer 1

To find the probability that a simple random sample of 49 protozoa will have a mean life expectancy of 47 or more days, calculate the z-score and use the standard normal distribution table.

Step-by-step explanation:

To find the probability that a simple random sample of 49 protozoa will have a mean life expectancy of 47 or more days, we need to calculate the z-score and then use the standard normal distribution table.

Step 1: Calculate the z-score

Z = (X - μ) / (σ /
`√(n)`)

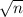X = 47 (mean life expectancy), μ = 46 (mean of the distribution), σ = 10.5 (standard deviation of the distribution), n = 49 (sample size)

Z = (47 - 46) / (10.5 /
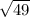`√(49)`) = 1.2857

Step 2: Use the standard normal distribution table to find the probability

From the standard normal distribution table, the cumulative probability for a z-score of 1.2857 is approximately 0.9008.

Therefore, the probability that a simple random sample of 49 protozoa will have a mean life expectancy of 47 or more days is approximately 0.9008 or 90.08%.

Answer 2

Answer: P(x ≥ 47) = 0.25

Step-by-step explanation:

Since the distribution of the life expectancies of a certain protozoan is normal, we would apply the formula for normal distribution which is expressed as

z = (x - µ)/σ

Where

x = life expectancies of the certain protozoan.

µ = mean

σ = standard deviation

n = number of samples

From the information given,

µ = 46 days

σ = 10.5 days

n = 49

The probability that a simple random sample of 49 protozoa will have a mean life expectancy of 47 or more days is expressed as

P(x ≥ 47) = 1 - P(x < 47)

For x = 47

z = (47 - 46)/(10.5/√49) = 0.67

Looking at the normal distribution table, the probability corresponding to the z score is 0.0.75

P(x ≥ 47) = 1 - 0.75 = 0.25