Answer:
the probability that the sample mean exceeds the W.H.O. minimum = 0.0059
Explanation:
Given -
The World Health Organization's (W.H.O.) recommended daily minimum of calories is 2600 per individual .
Mean
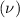 = 2460
= 2460
standard deviation
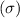 = 500
= 500
Sample size ( n ) = 81
Let
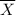 be the sample mean
be the sample mean
standard deviation of sample mean =
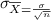 =
=
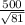 = 55.55
= 55.55
the probability that the sample mean exceeds the W.H.O. minimum =
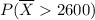 =
=
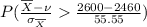
=
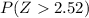
=
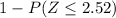
= 1 -.9941
= 0.0059