Question

Given AD = 24. Find the value of x and the length of each chord. If necessary, round your answers to the nearest hundredth.

Answer 1

`x\approx5.68\\\\CB\approx24.68`

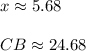
Explanation:

-The product of the segments of two chords intersecting each other in a circle is always equal:

`A.B=C.D`

-Given the chords AD and CB, we substitute to solve for x:

`CE* EB=AE * ED\\\\\therefore x* 19=6*(24-6)\\\\19x=108\\\\x=5.6842\approx5.68`

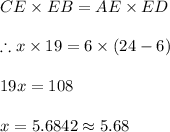
#Length CB is the sum of segment x and segment EB:

`CB=x+EB\\\\=19+5.68\\\\=24.68`

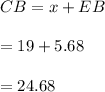
Hence, x is approximately 5.68 and CB is 24.68