Question

A study of one thousand teens found that the number of hours they spend on social networking sites each week is normally distributed with a mean of 20 hours. The population standard deviation is 2 hours. What is the 95% confidence interval for the mean?

Answer 1

The 95% confidence interval for the mean is lower confidence limit = 19.88, and upper confidence limit = 20.12. Some notations for confidence interval are (19.88, 20.12) or [19.88, 20.12].

Explanation:

The answer to this question is to find two values that define an interval in which we can consider there is, with a certain probability, the population's mean
`\\ \mu`.

We have here important information from the question:

• The size of the sample is "one thousand teens". So, n = 1000.
• The random variable "the number of hours they (the teens) spend on social networking sites each week" is normally distributed. In other words, this random variable follows a normal distribution.
• The value of the mean for this sample is
  `\\ \overline{x} =20`.
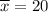• The population standard deviation
  `\\ \sigma =2\;hours`.
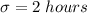• For a 95% confidence interval, we have a confidence coefficient of 1.96. The explanation for the latter is, roughly speaking, that we have to both side we have a remaining of 5%/2 or 0.05/2 = 0.025. The z-score corresponding to this probability is 1.96 (or -1.96, below the mean, and 1.96 above the mean. That is,
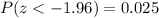  `\\ P(z< -1.96) = 0.025` and
  `\\ P(z>1.96) = 0.025`).

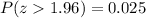Since we know that the random variable is normally distributed, the sample means are also normally distributed. Then, we can pose mathematically this problem as follows:

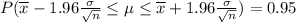`\\ P(\overline{x} - 1.96(\sigma)/(√(n)) \leq \mu \leq \overline{x} + 1.96(\sigma)/(√(n))) = 0.95` [1]

In this way, we have enough information to solve it:

`\\ \overline{x} = 20`.

`\\ \sigma = 2`.

`\\ n = 1000`.

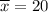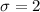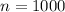Well, substituting each value in [1], we have:

`\\ P(20 - 1.96(2)/(√(1000)) \leq \mu \leq 20 + 1.96(2)/(√(1000))) = 0.95`

Then

`\\ P(20 - 1.96(2)/(31.62) \leq \mu \leq 20 + 1.96(2)/(31.62)) = 0.95`

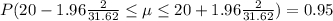
The value for

`\\ 1.96(2)/(31.62) \approx 1.96*0.06 \approx 0.12`

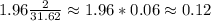
Therefore

`\\ P(20 - 0.12 \leq \mu \leq 20 + 0.12) = 0.95`

`\\ P(19.88 \leq \mu \leq 20.12) = 0.95`

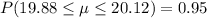
As a result, we can say that the 95% confidence interval for the mean is lower confidence limit = 19.88 and upper confidence limit = 20.12.

Note: some authors described these limits as (19.88, 20.12), while others as [19.88, 20.12].