Question

The figure is made up of a cylinder and a sphere which has been cut in half. The radius of each half sphere is 5 mm. What is the volume of the composite figure? Use 3.14 for Pi. Round to the nearest hundredth.

A cylinder and 2 half spheres. All have a radius of 5 millimeters. The cylinder has a height of 10 millimeters.

Recall the formulas V = B h and V = four-thirds pi r cubed
376.80 cubic millimeters
847.80 cubic millimeters
1,177.50 cubic millimeters
1,308.33 cubic millimeters

Answer 1

i agree 1,308.33

Explanation:

Answer 2

Volume of Solids

The volume of the composite figure is 1308.33 mm³

Explanation:

Radius of cylinder base r = 5 mm

height of cylinder h = 10 mm

Volume of cylinder =
`\pi r^(2) h`

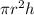
Volume of Sphere =
`(4)/(3) \pi r^(3)`

Volume of composite figure = Volume of cylinder + Volume of Sphere

V =
`\pi r^(2) h` +
`(4)/(3) \pi r^(3)\\`

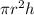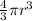
Volume of cylinder = 3.14 × 5 × 5 × 10 = 785 mm³

Volume of Sphere =
`(4)/(3)` × 3.14×5×5×5 = 523.33 mm³

Volume of the composite figure = 785 + 523.33 = 1308.33 mm³

Hence. the volume of the composite figure is 1308.33 mm³