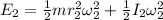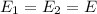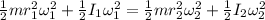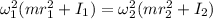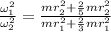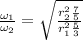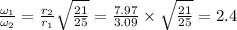Question

A sphere of radius 3.09 cm and a spherical shell of radius 7.97 cm are rolling without slipping along the same floor. The two objects have the same mass. If they are to have the same total kinetic energy, what should the ratio of the sphere's angular speed to the spherical shell's angular speed be?

Answer 1

2.4

Step-by-step explanation:

We are given that

`r_1=3.09 cm`

`r_2=7.97 cm`

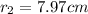
Let mass of each object =m

K.E of each object=E

We have to find the ration of sphere's angular speed to the spherical shell's angular speed.

Moment of inertia of sphere,
`I_1=(2)/(5)Mr^2_1`

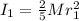
Moment of inertia of spherical shell,
`I_2=(2)/(3)Mr^2_2`

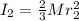
Linear speed,
`v=\omega r`

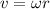
K.E of sphere ,
`E_1=(1)/(2)mr^2_1\omega^2_1+(1)/(2)I_1\omega^2_1`

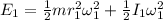
K.E of spherical shell,
`E_2=(1)/(2)mr^2_2\omega^2_2+(1)/(2)I_2\omega^2_2`

`E_1=E_2=E`

`(1)/(2)mr^2_1\omega^2_1+(1)/(2)I_1\omega^2_1=(1)/(2)mr^2_2\omega^2_2+(1)/(2)I_2\omega^2_2`

`\omega^2_1(mr^2_1+I_1)=\omega^2_2(mr^2_2+I_2)`

`(\omega^2_1)/(\omega^2_2)=(mr^2_2+(2)/(5)mr^2_2)/(mr^2_1+(2)/(3)mr^2_1)`

`(\omega_1)/(\omega_2)=\sqrt{(r^2_2(7)/(5))/(r^2_1(5)/(3))}`

`(\omega_1)/(\omega_2)=(r_2)/(r_1)\sqrt{(21)/(25)}=(7.97)/(3.09)* \sqrt{(21)/(25)}=2.4`