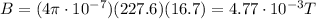Question

A 15.0 m \long copper wire, 2.20 mm in diameter including insulation, is tightly wrapped in a single layer with adjacent coils touching, to form a solenoid of diameter 2.10 cm (outer edge).a) What is the length of the solenoid?

b) What is the field at the center when the current in the wire is 16.7 A ?

Answer 1

a) 0.5 m

b)
`4.77\cdot 10^(-3) T`

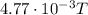
Step-by-step explanation:

a)

At the beginning, the length of the copper wire is:

L = 15.0 m

and the diameter (so, the thickness of each adjacent circle) is

`t=2.20 mm = 0.0022 m`

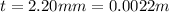
While the diameter of one circle of the solenoid is

`d=2.10 cm = 0.021 m`

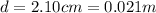
So the perimeter of one circle is

`p=\pi d=\pi (0.021)=0.0659 m`

So the number of complete circles in the solenoid is

`n=(L)/(p)=(15.0)/(0.0659)=227.6`

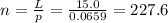
The tickness of one circle is
`t`, so the total length of the solenoid will be:

`L'=nt=(227.6)(0.0022)=0.5 m`

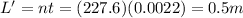
b)

The magnetic field at the center of a solenoid is given by

`B=\mu_0 n I`

where

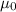`\mu_0` is the vacuum permeability

n is the number of turns of the solenoid

I is the current in the solenoid

Here we have:

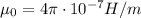`\mu_0 =4\pi \cdot 10^(-7)H/m` is the vacuum permeability

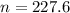`n=227.6` is the number of turns in the solenoid (calculated in part a)

I = 16.7 A is the current in the solenoid

Substituting, we find:

`B=(4\pi \cdot 10^(-7))(227.6)(16.7)=4.77\cdot 10^(-3) T`