Question

A medical equipment industry manufactures X-ray machines. The unit cost c

(the cost in dollars to make each X-ray machine) depends on the number of machines made. If x machines are made, then the unit cost is given by the function
c(x)=x^2-520x+72857. What is the minimum unit cost?
Do not round your answer

Answer 1

The minimum unit cost is $5257

Explanation:

Minimization

Given a function c(x), the minimum value of c can be found by computing the first derivative. Equating the first derivative to zero will provide the critical points, or candidate point to maximize or minimize the function. The second derivative criterion will make clear which type of point was obtained.

The cost in dollars to produce x machines is

`C(x)=x^2-520x+72857`

Find the first derivative

`C'(x)=2x-520`

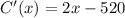
Equate to 0

`2x-520=0`

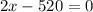
Solving:

`x=260`

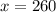
There must be produced 260 machines to minimize the cost. The minimum cost is

`C(260)=260^2-520\cdot 260+72857`

`C(260)=5257`

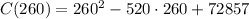
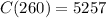
The minimum unit cost is $5257