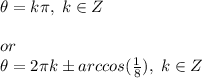Question

Solve the given equation. (Enter your answers as a comma-separated list. Let k be any integer. Round terms to three decimal places where appropriate. If there is no solution, enter NO SOLUTION.) 8 sin(2θ) − 2 sin(θ) = 0

Answer 1

`\theta=k\pi, \hspace{3}k\in Z\\\\ or\\\theta =2\pi k \pm arccos((1 )/(8) ), \hspace{3}k\in Z\\`

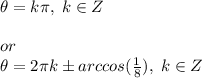
Explanation:

Factor constant terms:

`-2(-4sin(2\theta)+sin(\theta))=0`

Divide both sides by -2:

`sin(\theta)-4sin(2 \theta)=0`

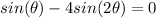
Expand trigonometric functions using the fact:

`sin(2 \theta) =2 sin(\theta) cos(\theta)`

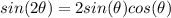
So:

`sin(\theta) -8sin(\theta)cos(\theta)=0`

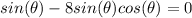
Factor sin(x) and constant terms and multiply both sides by -1:

`sin(\theta) (8cos(\theta)-1)=0`

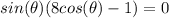
Split into two equations:

`(1)=8cos(\theta)-1=0\\\\(2)=sin(\theta)=0`

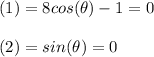
For (1)

Add 1 to both sides and divide both sides by 8:

`cos(\theta)=(1)/(8)`

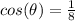
Take the inverse cosine of both sides:

`\theta =2\pi k \pm arccos((1 )/(8) ), \hspace{3}k\in Z`

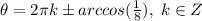
For (2)

Simply take the inverse sine of both sides

`\theta = k \pi, \hspace{3}k\in Z`

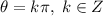
Therefore, the solutions are given by:

`\theta=k\pi, \hspace{3}k\in Z\\\\ or\\ \theta =2\pi k \pm arccos((1 )/(8) ), \hspace{3}k\in Z\\`