Question

A two sided hypothesis test at the alpha = 2% level failed to reject the null hypothesis that claimed that the population mean was equal to 21. What can you tell about 21 being included or not into different levels of confidence intervals? Mark the correct answer(s).

Answer 1

If the null hypothesis is rejected it implies that the null value of mean, i.e. 21 is not included in the interval.

Explanation:

The (1 - α)% confidence interval for population mean (μ) is:

`CI=\bar x\pm z_(\alpha/2)* (SD_(x))/(√(n))`

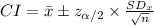
A hypothesis test's decision can be made according to the confidence interval concluded.

The decision rule is:

If the (1 - α)% confidence interval consists of the null value of the test then the null hypothesis will be accepted or else rejected.

The hypothesis in this case can be defined as follows:

H₀: The population mean was equal to 21, i.e. μ = 21.

Hₐ: The population mean was not equal to 21, i.e. μ ≠ 21.

The decision made was:

A two-sided hypothesis test at the α = 2% level failed to reject the null hypothesis that claimed that the population mean was equal to 21.

This implies that the (1 - α)% = 98% confidence interval for population mean does not includes the value 21.

Because only if the null hypothesis value is not included in the interval, that the null hypothesis will be rejected.

So, if the null hypothesis is rejected it implies that the null value of mean, i.e. 21 is not included in the interval.