Answer:
Power dissipated in resistor 532 ohm is 0.503 watt
Step-by-step explanation:
We have given in first case resistance
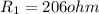
Power dissipated in this resistance is
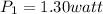
Power dissipated in the resistor is equal to
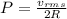
We have to find the power dissipated in the resistor is 1.30 watt
From the relation we can say that
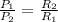
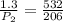
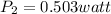
So power dissipated in resistor 532 ohm is 0.503 watt