Question

P(x < 21 | μ = 23 and σ = 3) enter the probability of fewer than 21 outcomes if the mean is 23 and the standard deviation is 3 (b) P(x ≥ 66 | μ = 50 and σ = 9) enter the probability of 66 or more outcomes if the mean is 50 and the standard deviation is 9 (c) P(x > 47 | μ = 50 and σ = 5) enter the probability of more than 47 outcomes if the mean is 50 and the standard deviation is 5 (d) P(17 < x < 24 | μ = 21 and σ = 3) enter the probability of more than 17 and fewer than 24 outcomes if the mean is 21 and the standard deviation is 3 (e) P(x ≥ 95 | μ = 80 and σ = 1.82) enter the probability of 95 or more outcomes if the mean is 80 and the standard deviation is 1.82

Answer 1

(a) The value of P (X < 21 | μ = 23 and σ = 3) is 0.2514.

(b) The value of P (X ≥ 66 | μ = 50 and σ = 9) is 0.0427.

(c) The value of P (X > 47 | μ = 50 and σ = 5) is 0.7258.

(d) The value of P (17 < X < 24 | μ = 21 and σ = 3) is 0.7495.

(e) The value of P (X ≥ 95 | μ = 80 and σ = 1.82) is 0.

Explanation:

The random variable X is Normally distributed.

(a)

The mean and standard deviation are:

`\mu=23\\\sigma=3`

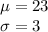
Compute the value of P (X < 21) as follows:

`P(X<21)=P((X-\mu)/(\sigma)<(21-23)/(3))`

`=P(Z<-0.67)\\=1-P(Z<0.67)\\=1-0.74857\\=0.25143\\\approx0.2514`

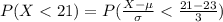
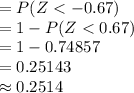
Thus, the value of P (X < 21 | μ = 23 and σ = 3) is 0.2514.

(b)

The mean and standard deviation are:

`\mu=50\\\sigma=9`

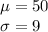
Compute the value of P (X ≥ 66) as follows:

Use continuity correction.

P (X ≥ 66) = P (X > 66 - 0.5)

= P (X > 65.5)

`=P((X-\mu)/(\sigma)>(65.5-50)/(9))`

`=P(Z>1.72)\\=1-P(Z<1.72)\\=1-0.9573\\=0.0427`

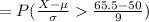
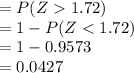
Thus, the value of P (X ≥ 66 | μ = 50 and σ = 9) is 0.0427.

(c)

The mean and standard deviation are:

`\mu=50\\\sigma=5`

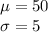
Compute the value of P (X > 47) as follows:

`P(X>47)=P((X-\mu)/(\sigma)>(47-50)/(5))`

`=P(Z>-0.60)\\=P(Z<0.60)\\=0.7258`

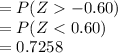
Thus, the value of P (X > 47 | μ = 50 and σ = 5) is 0.7258.

(d)

The mean and standard deviation are:

`\mu=21\\\sigma=3`

Compute the value of P (17 < X < 24) as follows:

`P(17<X<24)=P((17-21)/(3)<(X-\mu)/(\sigma)<(24-21)/(3))`

`=P(-1.33<Z<1)\\=P(Z<1)-P(Z<-1.33)\\=0.8413-0.0918\\=0.7495`

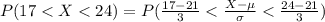
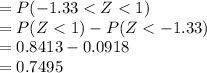
Thus, the value of P (17 < X < 24 | μ = 21 and σ = 3) is 0.7495.

(e)

The mean and standard deviation are:

`\mu=80\\\sigma=1.82`

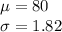
Compute the value of P (X ≥ 95) as follows:

Use continuity correction:

P (X ≥ 95) = P (X > 95 - 0.5)

= P (X > 94.5)

`=P((X-\mu)/(\sigma)>(94.5-80)/(1.82))`

`=P(Z>7.97)\\=1-P(Z<7.97)\\=1-(\approx1)\\=0`

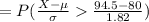
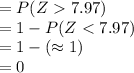
Thus, the value of P (X ≥ 95 | μ = 80 and σ = 1.82) is 0.