Complete Question

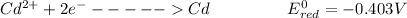
A galvanic cell based on these half-reactions is set up under standard conditions where each solutions is 1.00 L and each electrode weighs exactly 100.0 g. How much will the Cd electrode weigh when the non-standard potential of the cell is 0.03305 V?
Answer:
The mass is M= 117.37g
Step-by-step explanation:
The overall reaction is as follows
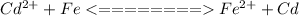
The reaction is this way because the potential of
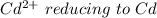 is higher than the potential of
is higher than the potential of
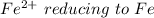 so the the Fe would be oxidized and
so the the Fe would be oxidized and
 would be reduced
would be reduced
At equilibrium the rate constant of the reaction is
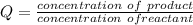
![= ([Fe^(2+)[Cd]])/([Cd^(2+)][Fe])](https://img.qammunity.org/2021/formulas/physics/college/el1pg8yq1stp08gvnbczvmwetulbovqyt3.png)
The Voltage of the cell
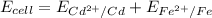
Substituting the given values into the equation
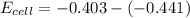
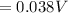
The voltage of the cell at any point can be calculated using the equation

Where
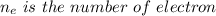
Substituting for Q
![E = E_(cell) - (0.059)/(n_e) ([Fe^(2+)[Cd]])/([Cd^(2+)][Fe])](https://img.qammunity.org/2021/formulas/physics/college/jrvwabfib4xc7ayq0jh0g3km6fgqnrmx2h.png)
When E = 0.03305 V
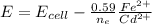
Since we are considering the Cd electrode the equation becomes
![E= E_(cell) - (0.059)/(n_e) [(1)/(Cd^(2+)) ]](https://img.qammunity.org/2021/formulas/physics/college/qdd9bqd8xnprca3h1leq5wqvnlxar72j3c.png)
Substituting values and making [
 ] the subject
] the subject
![[Cd^(2+)] =\frac{1}{e^{[(0.03305- 0.038)/((0.059 )/(2) )] }}](https://img.qammunity.org/2021/formulas/physics/college/xdygq9n7uc0sv69pnod0su2vunykkdpy6l.png)

Given from the question that the volume is 1 Liter
The number of mole = concentration * volume
= 0.8455 * 1
= 0.8455 moles
At the standard state the concentration of
 is =1 mole /L
is =1 mole /L
Hence the amount deposited on the Cd electrode would be
= Original amount - The calculated amount
= 1 - 0.8455
= 0.1545 moles
The mass deposited is mathematically represented as
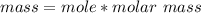
The Molar mass of Cd
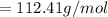
Mass
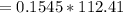

Hence the total mass of the electrode is = standard mass + calculated mass
M= 100+ 17.37
M= 117.37g