Question

Use a normal approximation to find the probability of the indicated number of voters. In this​ case, assume that 145 eligible voters aged​ 18-24 are randomly selected. Suppose a previous study showed that among eligible voters aged​ 18-24, 22% of them voted. Probability that fewer than 34 voted The probability that fewer than 34 of 145 eligible voters voted is nothing.

Answer 1

Explanation:

Using a standard approximation to calculate the likelihood of the number of electors stated. Suppose, in this scenario, that 185 registered voters aged 18-24 are randomly chosen. Suppose a recent survey found that 22 per cent of registered citizens aged 18-24 voted.

Mean = np = 0.22*185 = 40.7

std =
`√((npq))` =
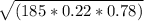`√((185*0.22*0.78) )` = 5.634

Probability that fewer than 46 voted

Binomial need:: P(x < 46)

Normal approx need:: P(x < 46.5)

P(46.5) = P(z < z)

= ( 46.5 - 40.7) / 5.634 = 5.8 / 5.634 = 0.8484

The probability that fewer than 34 of 145 eligible voters voted is 0.8484.