Question

The Federal Reserve System publishes data on family income based on its Survey of Consumer Finances. When the head of the household has a college degree, the mean before-tax family income is $ 84,950. Suppose that 70% of the before-tax family incomes when the head of the household has a college degree are between $74,800 and $95,100 and that these incomes are normally distributed. What is the standard deviation of before-tax family incomes when the head of the household has a college degree?

Answer 1

The standard deviation of before-tax family incomes when the head of the household has a college degree is $5,075.

Explanation:

The different types of the measures of dispersion are:

• Variance
• Standard deviation
• Interquartile Range
• Range

The standard deviation is the root mean square of the sum of deviations from the mean of the data.

`\sigma =\sqrt{(\sum (X_(i)-\mu)^(2))/(N)}`

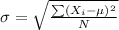
The standard deviation of a data set represents the value by which the data values are away from the mean. It is the best measure of dispersion because it considers all the values in the data set for the calculation.

The standard deviation of a data set can be estimated from the range of the data.

The standard deviation is one-fourth of the range.

`\sigma=(Range)/(4)`

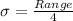
It is provided that the head of the household has a college degree are between $74,800 and $95,100.

Compute the range of the distribution as follows:

`Range= Max.-Min.\\=95100-74800\\=20300`

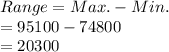
Compute the standard deviation as follows:

`\sigma=(Range)/(4)=(20300)/(4)=5075`

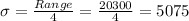
Thus, the standard deviation of before-tax family incomes when the head of the household has a college degree is $5,075.