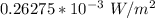Question

A certain loudspeaker system emits sound isotropically (uniformly in all directions) with a frequency of 1,054 Hz and an intensity of 6.429 mW/m2 at a distance of 7.945 m. Assume that there are no reflections. What is the intensity in 10-3 W/m2 at 39.3 m? (you don't need to write the power/prefix and unit

Answer 1

The intensity in 10-3 W/m2 at 39.3 m is
`0.26275*10^(-3)\ W/m^2`

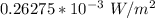
Step-by-step explanation:

Given Data:

frequency=1,054 Hz

intensity=6.429 mW/m^2

distance=7.945 m.

Required:

intensity in 10^-3 W/m^2 at 39.3 m=?

Solution:

Intensity at distance r from point source which is emitting sound waves of power P is given by the following formula:

Intensity=I=
`(P)/(4\pi r^2)`

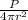
Where:

P is the power

r is the distance

`(I_1)/(I_2)=((P)/(4\pi r_1^2))/((P)/(4\pi r_2^2)) \\(I_1)/(I_2)=(r_2^2)/(r_1^2) \\I_2=I_1*(r_1^2)/(r_2^2)`

`r_1= 7.945 m\\r_2= 39.3 m\\I_2=6.429*10^(-3) *(7.945^2)/(39.3^2)`

`I_2=0.00026275\ W/m^2\\I_2=0.26275*10^(-3)\ W/m^2`

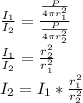
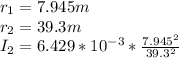
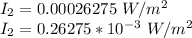
The intensity in 10^-3 W/m2 at 39.3 m is
`0.26275*10^(-3)\ W/m^2`