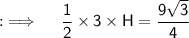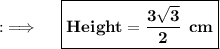Question

Find the height and area of the equilateral triangle ​

Answer 1

As here we are given with an equilateral triangle, whose side is 3 cm, and we need to find the height and area of the equilateral triangle. So, for this let's recall that, the area of any equilateral triangle with side a is given by ;

• 
  `{\boxed{\bf{Area_((Equilateral\:\: Triangle))=(√(3))/(4)a^(2)}}}`

So, if we substitute a = 3, in our Formula, it will yield to

`{:\implies \quad \sf Area_((Equilateral\:\:Triangle))=(√(3))/(4)(3)^(2)}`

`{:\implies \quad \sf Area_((Equilateral\:\:Triangle))=(√(3))/(4)(9)}`

`{:\implies \quad \boxed{\bf{Area_((Equilateral\:\:Triangle))=(9√(3))/(4)\:\:cm^(2)}}}`

Now, as we know that, for any triangle we also have a formula that is ;

• 
  `{\boxed{\bf{Area_((Triangle))=(1)/(2)* Base* Height}}}`

Now, Here as the triangle is equilateral, so it's base will just be same 3, and if we let height be H, so we will be having

`{:\implies \quad \sf (1)/(2)* 3* H=(9√(3))/(4)}`

`{:\implies \quad \sf H=(9√(3))/(4)* \frac23}`

`{:\implies \quad \boxed{\bf{Height=(3√(3))/(2)\:\:cm}}}`