Question

The time college students spend on the internet follows a Normal distribution. At Johnson University, the mean time is 5 hrs with a standard deviation of 1.2 hrs. What is the probability that the average time 100 random students on campus will spend more than 5 hours on the internet

Answer 1

The probability that the average time 100 random students on campus will spend more than 5 hours on the internet is 0.5

Explanation:

We are given that . At Johnson University, the mean time is 5 hrs with a standard deviation of 1.2 hrs.

Mean =
`\mu = 5 hours`

Standard deviation =
`\sigma = 1.2 hours`

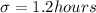
We are supposed to find the probability that the average time 100 random students on campus will spend more than 5 hours on the internet i.e. P(X>5)

`Z=(x-\mu)/(\sigma)`

`Z=(5-5)/(1.2)`

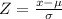
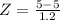
Z=0

P(X>5)=1-P(X<5)=1-P(Z<0)=1-0.5=0.5

Hence the probability that the average time 100 random students on campus will spend more than 5 hours on the internet is 0.5