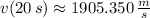Question

A rocket in deep space has an empty mass of 150 kg and exhausts the hot gases of burned fuel at 2500 m/s. It is loaded with 600 kg of fuel, which it burns in 30 s. What is the rocket’s speed 10 s, 20 s, and 30 s after launch?

Answer 1

`v(10\,s) \approx 775.387\,(m)/(s)`

`v(20\,s)\approx 1905.350\,(m)/(s)`

`v(30\,s) \approx 4023.595\,(m)/(s)`

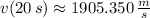
Step-by-step explanation:

The speed of the rocket is given the Tsiolkovsky's differential equation, whose solution is:

`v (t) = v_(o) - v_(ex)\cdot \ln (m)/(m_(o))`

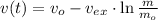
Where:

`v_(o)` - Initial speed of the rocket, in m/s.

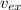`v_(ex)` - Exhaust gas speed, in m/s.

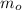`m_(o)` - Initial total mass of the rocket, in kg.

`m` - Current total mass of the rocket, in kg.

Let assume that fuel is burned linearly. So that,

`m(t) = m_(o) + r\cdot t`

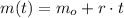
The initial total mass of the rocket is:

`m_(o) = 750\,kg`

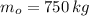
The fuel consumption rate is:

`r = -(600\,kg)/(30\,s)`

`r = -20\,(kg)/(s)`

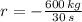
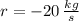
The function for the current total mass of the rocket is:

`m(t) = 750\,kg - (20\,(kg)/(s) )\cdot t`

The speed function of the rocket is:

`v(t) = - 2500\,(m)/(s)\cdot \ln (750\,kg -(20\,(kg)/(s) )\cdot t)/(750\,kg)`

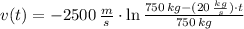
The speed of the rocket at given instants are:

`v(10\,s) \approx 775.387\,(m)/(s)`

`v(20\,s)\approx 1905.350\,(m)/(s)`

`v(30\,s) \approx 4023.595\,(m)/(s)`