Question

Find the length of chord QS

Answer 1

Given:

QW = 12 and WS = 4x + 1

PW = 14 and WR = 3x + 3

To find:

The length of the chord QS.

Solution:

If two chords intersect inside a circle, then the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord.

`\Rightarrow QW \cdot WS= PW\cdot WR`

`\Rightarrow 12 \cdot (4x+1)=14 \cdot (3x+3)`

`\Rightarrow 48x+12= 42x+42`

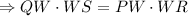
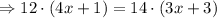
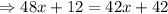
Subtract 12 from both sides.

`\Rightarrow 48x+12-12= 42x+42-12`

`\Rightarrow 48x= 42x+30`

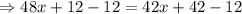
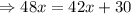
Subtract 42x from both sides.

`\Rightarrow 48x-42x= 42x+30-42x`

`\Rightarrow 6x= 30`

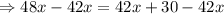
Divide by 6 on both sides, we get

⇒ x = 5

QS = QW + WS

`=12+4x+1`

`=12+4(5)+1`

`=13+20`

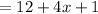
= 43

The length of QS is 43.