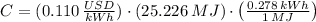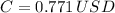Answer:
a)
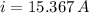 , b)
, b)
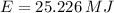 , c)
, c)
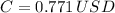
Step-by-step explanation:
a) Let assume that electric motor is single-phase and operates in DC-mode, so that mechanical power output is:
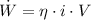
The current delivered to the motor is:
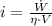
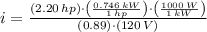
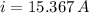
b) The power delivered to the motor is:
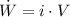
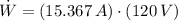
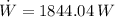
The energy delivered to the motor during 3.80 hours of operation is:
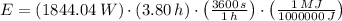
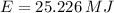
c) The cost to run the motor is: