Question

We want to focus on the time for navigation entry. For 24 younger adults (21-36 years), the average time for navigation entry was 31.4 seconds versus 40 seconds for the 24 participants in the older group (55-75 years). Standard deviations are not given, so we estimate the younger group at 0.99 seconds and the older group at 1.04 seconds. Test, using a 5% significance level, to see if there is evidence that the younger group have a lower mean time in seconds than the older group. 1. Write the correct null and alternative hypotheses.

Answer 1

We conclude that the younger group have a lower mean time in seconds than the older group.

Explanation:

We are given that for 24 younger adults (21-36 years), the average time for navigation entry was 31.4 seconds versus 40 seconds for the 24 participants in the older group (55-75 years).

Standard deviations are not given, so we estimate the younger group at 0.99 seconds and the older group at 1.04 seconds.

We have to conduct a hypothesis test to see whether the younger group have a lower mean time in seconds than the older group.

Let
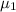`\mu_1` = population mean time for navigation entry for younger groups

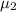`\mu_2` = population mean time for navigation entry for older groups

SO, Null Hypothesis,
`H_0` :
`\mu_1 \geq \mu_2` or
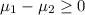`\mu_1-\mu_2\geq0` {means that the younger group have a mean time in seconds higher than or equal to the older group}

Alternate Hypothesis,
`H_a` :
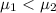`\mu_1< \mu_2` or
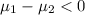`\mu_1-\mu_2 < 0` {means that the younger group have a lower mean time in seconds than the older group}

The test statistics that will be used here is Two-sample t test statistics as we don't know about the population standard deviations;

T.S. =
`\frac{(\bar X_1 - \bar X_2)-(\mu_1-\mu_2)}{s_p \sqrt{(1 )/(n_1) +(1 )/(n_2)} }` ~
`t__n__1+n_2-_2`

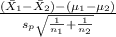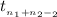
where,
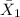`\bar X_1` = sample average time for navigation entry for younger adults (21-36 years) = 31.4 seconds

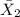`\bar X_2` = sample average time for navigation entry for older adults (55-75 years) = 40 seconds

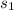`s_1` = standard deviation for 24 younger adults = 0.99 seconds

`s_2` = standard deviation for 24 participants in the older group = 1.04 seconds

`n_1` = sample size of younger adults = 24

`n_2` = sample size of older adults = 24

Here,
`s_p = \sqrt{((n_1-1)s_1^(2)+(n_2-1)s_2^(2) )/(n_1+n_2-2) }` =
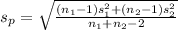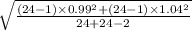`\sqrt{((24-1)* 0.99^(2)+(24-1)* 1.04^(2) )/(24+24-2) }` = 1.015

So, test statistics =
`\frac{(31.4-40)-(0)}{1.015 * \sqrt{(1 )/(24) +(1 )/(24)} }` ~
`t_4_6`

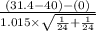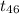
= -29.35

So, at 0.05 level of significance, the t table gives critical value of -1.6792 at 46 degree of freedom for one-tailed test. Since our test statistics is way less than the critical value of t so we have sufficient evidence to reject null hypothesis as it will fall in the rejection region.

Therefore, we conclude that the younger group have a lower mean time in seconds than the older group.