Question

A thin disk of mass 2.2 kg and radius 61.2 cm is suspended by a horizonal axis perpendicular to the disk through its rim. The disk is displaced slightly from equilibrium and released. The acceleration of gravity is 9.81 m/s2. Find the period of the subsequent simple harmonic motion. Answer in units of s.

Answer 1

Answer: The period of the subsequent simple harmonic motion is 1.004 sec.

Step-by-step explanation:

The given data is as follows.

Mass of disk (m) = 2.2 kg, radius of the disk (r) = 61.2 cm,

Formula to calculate the moment of inertia around the center of mass is as follows.

`I_(cm) = (1)/(2)mr^(2)`

=
`(1)/(2) * 2.2 kg * (61.2)^(2)`

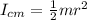
= 0.412
`kg m^(2)`

Also,

Distance between center of mass and axis of rotation (d) = r = 0.612 m

Moment of inertia about the axis of rotation (I)

I =
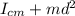
`I_(cm) + md^(2)`

I =
`0.412 + (2.2) * (0.612)^(2)`

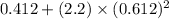
= 0.339
`kgm^(2)`

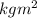
Now, we will calculate the time period as follows.

T =
`2\pi sqrt{(I)/(mgd))`

T =
`2 * 3.14 sqrt{((0.339)/(2.2 * 9.8 * 0.612)`

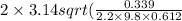
T = 1.435 sec

T =
`2 * 3.14 * 0.16`

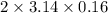
= 1.004 sec

Thus, we can conclude that the period of the subsequent simple harmonic motion is 1.004 sec.